От графика к формуле

Полином можно "гладко" дифференцировать n раз, но разброс его значений между точками может быть очень большим — сглаживание великолепное, но интерполяции, особенно на краях— никакой. Компромиссным вариантом решения этой проблемы и являются сплайны (см. рис. 4.3 и 4.7), комбинирующие линейную и полиномиальную интерполяции: внутри интервала берутся четыре точки, через которые проводится кубический полином. От него при необходимости можно "гладко" взять первую и вторую производные, которые, в свою очередь, необходимы для решения, например, оптимизационных задач градиентными методами (см. главу 3). На концах интервала ("у обрыва") точек не четыре, а три или две, и здесь сплайн-интерполяция ведет себя по-разному— в зависимости от приставки корня слова "spline" данной встроенной функции: lspline— линейная, pspiine— параболическая и cspline — кубическая (рис. 4.10).

Рис. 4.10. 20-экстраполяция сплайном за пределами последней точки

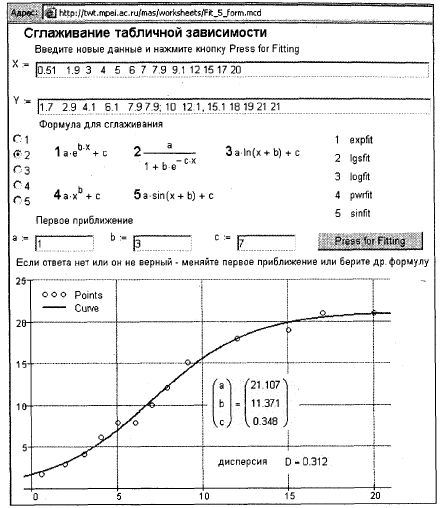
Рис. 4.11. Сглаживание табличной зависимости по пяти формулам в Интернете