Оптимизация габаритов объемных тел 3.1.1. Гремим пожарными ведрами

Из круглой жестянки по несложной технологии изготавливается пожарное ведро] (см. п. 1 на рис. 3.1): вырезается сектор, затем полученная выкройка сворачивается в конус (точка а подтягивается к точке с), а шов сваривается (паяется).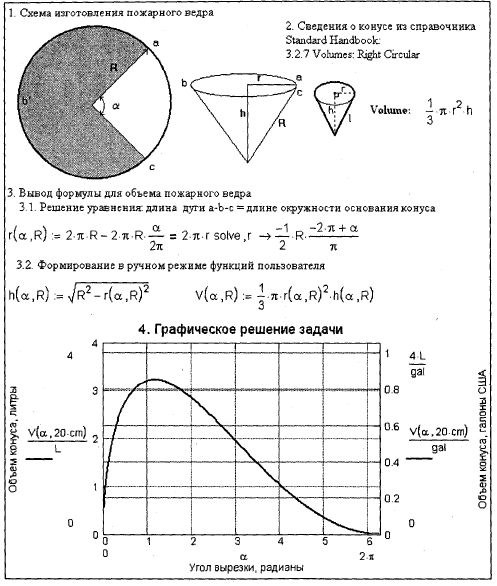

Рис. 3.1. Задача о пожарном ведре: схема решения

Требуется найти угол вырезки, при котором объем ведра будет максимальным.

И при решении данной задачи мы должны вывести зависимость объема ведра v от угла вырезки а. Далее можно взять первую производную от этой функции, приравнять ее к нулю и найти корень полученного уравнения. Не обойтись тут и без второй производной, если нужно убедиться, что найденное решение — максимум, а не минимум или точка перегиба, где, как помнит читатель из курса математического анализа, первая производная также равна нулю. Жестянщик, которому поручат сделать такое пожарное ведро, скорее всего, незнаком с математическим анализом, азы которого мы только что изложили. Но в среде Mathcad поставленная задача вполне окажется по плечу "компьютеризированному" жестянщику.

Рисунок заготовки ведра и самого ведра в п. 1 на рис. 3.1 сделан с помощью графического редактора Paint и перенесен в Mathcad-документ через буфер обмена (см. рис. 1.58).

В п. 2 на рис. 3.1 скопированы данные о геометрии конуса из стандартного справочника Mathcad, который удобен тем, что входит в состав пакета и всегда находится под рукой (см. рис. 1.4). Перенос данных из справочника в Mathcad-документ также автоматизирован, что исключает их искажение — переписывая формулу из книги, немудрено и ошибиться.

В п. 3 на рис. 3.1 записаны операторы символьных (аналитических) преобразований: оператором solve решается алгебраическое уравнение, а тандемом r(α,R):=…→ формируется функция пользователя с именем r (п. 3.1). Далее формируются две другие функции: h и v (п. 3.2). Зависимости выводятся из несложной геометрии круга и конуса: дуга abc выкройки (2πR - 2πRα/π) становится длиной окружности в основании конуса (2πr), a высота конуса h, радиус его основания r и радиус заготовки r — это стороны прямоугольного треугольника, длины которых связаны теоремой Пифагора.

Примечание

Решение задачи на компьютере — это только один из этапов общего процесса решения задачи. Другой немаловажный этап — это постановка задачи человеком, перекладывание словесного описания задачи на язык математики и компьютера.

Прежде чем искать максимум функции, необходимо убедиться, что он существует. Лучший же способ увидеть максимум — просмотреть график функции. В среде Mathcad, как уже отмечалось, есть семь видов графиков (см. разд. 1.6), первый из которых (X-Y Plot (Декартов график)) отображен на рис. 3.1. Здесь график построен по "двухшаговой" технологии: задается вид функции и сразу отдается команда на вставку графика в Mathcad-документ. По умолчанию аргумент графика меняется от -10 до 10. После построения наброска графика его нужно будет отформатировать— изменить разброс аргумента и другие установки по умолчанию.

На графике в районе угла, равного 1 радиан (60—70 угловых градусов), отчетливо виден максимум функции. Как его уточнить?

На рис. 3.2 показано аналитическое (символьное) решение данной задачи через поиск корней уравнения: первая производная функции v(α, r) равна нулю. Таких точек у функции v(α, R) оказалось три— два максимума (α1 и α2)^2 и один локальный минимум (α0). Задача решалась так. Сначала оператором ■ solve, ■→ выводились на дисплей корни уравнения v (a, R) =0, а после того, как стало ясно, что уравнение в среде Mathcad решается и корней три, то оператор ■ solve, ■ → встраивался в оператор ■ : = ■, в левый операнд которого вставлен вектор с тремя элементами по числу найденных корней. Элементы вектора хранят переменные α0, α1 и α2 (здесь не числовые, а текстовые индексы α0 → α0), третья из которых α2 — наш искомый ответ, который выводится на печать в угловых градусах и накладывается маркером на график функции v (α, R) при r=20 см. При аналитическом решении задачи в отличие от графического или численного (см. рис. 3.3) переменная r может оставаться пустой и не принимать никакого числового значения. На то оно и символьное решение. Это одно из преимуществ символьной математики — значение переменной r не влияет на решение и его можно не задавать. При численном же решении задачи (см. рис. 3.3, 3.4 и 3.7) всегда будет оставаться открытым вопрос, а не изменится ли решение, если изменить значение переменной r либо какой-нибудь другой константы. Беглый взгляд на задачу говорит о том, что нет, не изменится. Но в других задачах (см. рис. 3.12 и 3.13), как правило, такого однозначного ответа с "первого, беглого" взгляда не видно. Но если перейти от "одноведерной" к "двухведерной" задаче — задаче, когда из круглой заготовки вырезаются два ведра— к поиску корней производной функции v(α, R) + V(2π-α, r), to символьная математика Mathcad даст сбой. Нужно переходить к численным методам, которые, как правило, выдают один ответ из множества возможных и не с абсолютной, а с ограниченной точностью.

Самый старый способ численного поиска максимумов и минимумов в среде Mathcad, работавший еще в DOS-версиях,— это модификация блока