Дифференциальные уравнения

Описанная задача об эпидемии сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений первого порядка относительно Двух неизвестных функций Больные (t) И Здоровые (t) .

Больные'(t) = Больные(t) • (Пр • Здоровые(t)-1) Здоровые'(t) = -Пр • Больные(t) • Здоровые(t)

На рис. 5.1 по сути реализован метод Эйлера]0 с единичным шагом интегрирования At.

Больные(t+1) = Больныес + ∆t • Больные't Здоровые(t+1) = Здоровыеt + ∆t • Здоровые't

В среде Mathcad до версий PLUS 5.0 дифференциальные уравнения без особых ухищрений можно было решать только методом Эйлера, который имеет низкую точность и производительность (плата за простоту). Инструментарий для решения дифференциальных уравнений (систем) различного порядка и различными методами появился в арсенале Mathcad PLUS 6.0. В него входили 13 встроенных функций (Bustoer, bustoer, bvalfit, multigird, relax, Rkadapt, rkadapt, rkfixed, sbval, Stiffb, stiffb, Stiffr И stiffr), работа одной из которых (самой, наверно, востребованной rkfixed — метод Рунuе — Кутты (rk) четвертого порядка с фиксированным (fixed) шагом интегрирования) показана на рис. 5.2. У этой функции пять аргументов:

вектор (скаляр при одном уравнении) начальных значений искомых решений (задача Коши);

- абсцисса начальной точки интегрирования;

- абсцисса конечной точки интегрирования;

- число шагов интегрирования;

- функция-вектор правых частей системы.

Примечание

Обычно тут пишут Х0 и Х1 (два элемента одного вектора), но мы написали хитрее и понятнее: ЛюдиБольные и Люди Здоровые, предварительно определив, что индекс Больные равен нулю, а индекс Здоровые — единице (см. для сравнения рис. 5.12, где обошлись без этой хитрости).

Функция rkfixed возвращает в матрицу (у нас она имеет имя м) с P+1 столбцами и п строками (р — количество уравнений или порядок уравнения — у нас P=2) таблицу решений системы: первый (вернее, нулевой) столбец — это значения аргумента t (их задает пользователь через величины tнач, tкон и n), а последующие столбцы — значения ординат решения.

На рис. 5.2 три столбца матрицы M (время, число больных и число здоровых) разнесены по отдельным векторам и отображены графически, что позволяет, как и на рис. 5.1, проследить динамику развития эпидемии.

На рис. 5.2 получены несколько иные результаты, чем на рис. 5.1, хотя характер кривых сохранился. Это объясняется различными значениями точности расчетов (на рис. 5.1 делалось 13 шагов интегрирования, а на рис. 5.2 — 500 шагов) и различными примененными методиками (Эйлер против Рунге и Кутты"). На рис. 5.3 отображена страница Интернета с адресом http://twt.mpei.ac.ru/mas/worksheets/Euler.mcd, где можно провести сравнение этих двух методов (Euler и Runge — Kutta).

Из рис. 5.3 видно, что при малом числе шагов интегрирование (n=30) "Эйлера заносит на поворотах". Исправить эту ошибку можно через увеличение п. Но не всегда. Во-первых, это может недопустимо замедлить расчет, а во-вторых, есть класс задач, где такое механическое увеличение приводит к срыву решения задачи. На отмеченном сайте можно увидеть и Mathcad-программы, раскрывающие методы Эйлера и Рунге — Кутты четвертого порядка.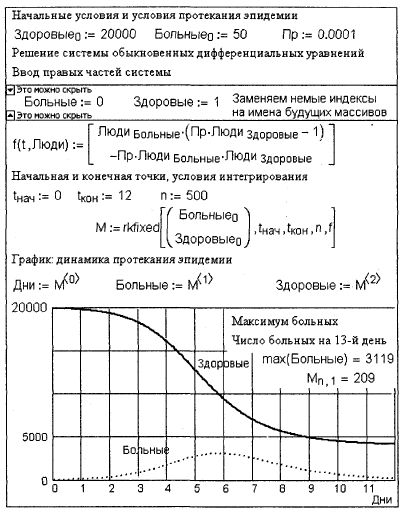

Рис. 5.2. Задача об эпидемии — решение системы дифференциальных уравнений с помощью функции rkf ixed

Можно решить задачу более точно и более быстро, если уменьшать шаг (у нас это At) там, где производная меняется быстро, и увеличивать шаг там, где она ведет себя более спокойно. Для этого предусмотрена функция Rkadapt (от англ. adaption — адаптация). Но, несмотря на то что при решении дифференциального уравнения функция Rkadapt использует непостоянный шаг, она, тем не менее, представит ответ для точек, находящихся на одинаковом расстоянии, заданном пользователем.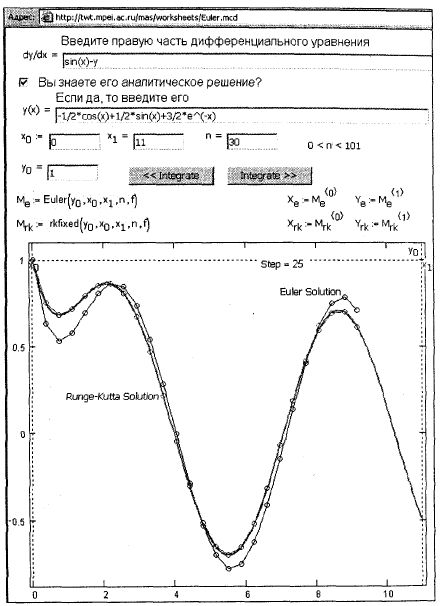

Рис. 5.3. Методы Эйлера и Рунге — Кутты с фиксированным шагом в Интернете

Аргументы и матрица, возвращаемая функцией Rkadapt, такие же, как при rkfixed. На рис. 5.4 отображена еще одна страница Интернета с адресом

http://twt.mpei.ac.ru/mas/worksheets/rkadapt.mcd, где читатель может проследить "динамику" решения дифференциального уравнения при переменном (подстраивающемся) шаге интегрирования. Там же можно увидеть и соответствующую Mathcad-программу метода Rkadapt.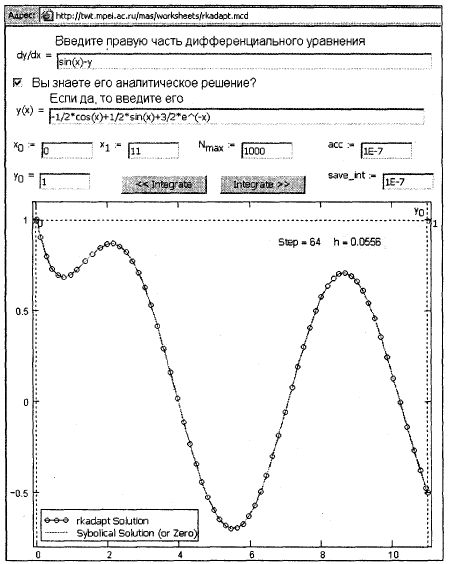

Рис. 5.4. Метод Рунге — Кутты с переменным шагом в Интернете