Функции двух аргументов

Можно привести еще множество примеров, толкающих к тому, что аргументами функций, перечисленных в табл. 4.2 и 4.3, могут и должны быть не только двоичные, но и вещественные числа, плавно меняющиеся от нуля до единицы. И возвращать функции, перечисленные в табл. 4.2 и 4.3, должны вещественные значения, опять же плавно меняющиеся от нуля до единицы. Вот как, например, можно задать "плавную" функцию отрицания (рис. 4.26):

Not(а):=1-а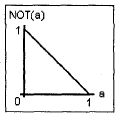

Рис. 4.26. Графическая иллюстрация плавного изменения функции отрицания

"Плавная" конъюнкция и "плавная" дизъюнкция получаются сами собой, если вспомнить о том, что одно из обозначений конъюнкции— это min, a дизъюнкции — max (см. решение задачи об оптимальном пожарном ведре в разд. 3.8):

And(a, b):=min(a, b) Or (a, b) :=min(a, b)

Несложно задать и другие "плавные" двоичные функции:

Eqv(a, b):=l-|a - b| XOr(a, b):=l-EQV(a, b)

Для иллюстрации функций двух переменных требуются уже не линии, а поверхности. На рис. 4.27 показаны, если так можно выразиться, заглавные

"булевы Кубики"---- поверхности "плавныхх" двоичных функций (And, Or, Eqv,

хог), которые при двоичных аргументах полностью повторяют работу своих традиционных "четких" аналогов, но при вещественных аргументах возвращают также вещественные значения, плавно меняющиеся от 0 до 1.

Если вращать кубики, показанные на рис. 4.27, то можно увидеть все 16 функций из табл. 4.3:

вращаем кубик And вокруг вертикальной оси — получаем функции f7, f9 и f10 (три единицы внизу, а одна наверху);

вращаем кубик Or (его можно получить, перевернув вверх ногами кубик And) вокруг вертикальной оси — получаем функции f5, f6 и f8 (три единицы наверху, а одна внизу);

вращаем кубик функции f14 вокруг вертикальной оси— получаем функции f11, f12 и f13 (две единицы внизу, а две наверху);

переворачиваем вверх дном кубик функции f16 (четыре единицы внизу) — получаем функцию f 15 (четыре единицы наверху).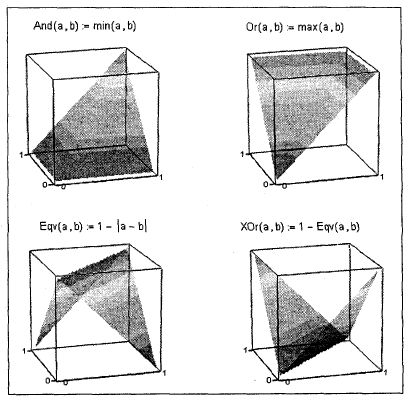

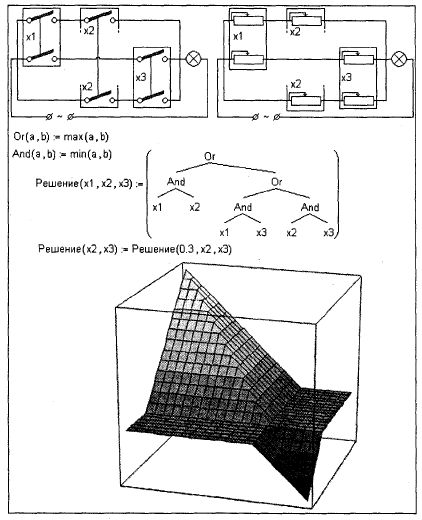
Рис. 4.27. Булевы кубики

4.4.4. Функции многих аргументов

На рис. 4.28 показано формирование в среде Mathcad "плавной" функции трех аргументов, возвращающей решение жюри присяжных, которые могутnвыдавать уже не "черно-белые" ответы (виновен— невиновен), а... "цветные": виновен на 30%, невиновен на 70%, например. В электрическом аналоге машинки для голосования выключатели заменены на реостаты.

Рис. 4.28. Машинка для нечеткого (мягкого, рейтингового) голосования

Функция Решение, показанная на рис. 4.28, при двоичных аргументах возвращает двоичный ответ, а при вещественных — вещественный, естественно.

Здесь же показан соответствующий "булев кубик" при а=0.3 — мы видим гибрид конъюнкции с дизъюнкцией: мнение одного члена жюри переводит вердикт из области or в область And.