Дифференциальные уравнения в частных производных

Решением дифференциальных уравнений в частных производных в общем случае будут функции не одного, а нескольких аргументов, производные по которым (частные производные) и формируют исходные уравнения. Здесь, как и в случае с обыкновенными (одноаргументными) дифференциальными уравнениями (см. предыдущий раздел), в среде Mathcad "зарождались" (Mathcad 6.0 PLUS) и "развивались" (Mathcad 11) частные и общие инструменты решения. Так на рис. 5.24 показана работа встроенной функции relax, которая появилась еще в Mathcad 6.0 PLUS, решающей уравнение Пуассона.

На рис. 5.24 сделана попытка моделирования в среде Mathcad процесса теплообмена на одной из плат компьютера с тремя микросхемами (чипами), работа которых сопровождается тепловыделением, рели правильно заполнить аргументы функции relax значениями (векторами и матрицами) с начальными условиями, то она возвратит температурное поле платы компьютера, которое на рис. 5.24 отображено графиком линий уровня и трехмерной поверхностью.

Более наглядно решение дифференциального уравнения в частных производных ведется через функцию Pdesoive (р от англ. partial— частичное, частное; de — дифференциальное уравнение и solve — решать), появившуюся в Mathcad 11. На рис. 5.25 функция Pdesoive возвращает решение другой тепловой задачи — остывание цилиндрического стержня.

Рис. 5.24. Моделирование температурного поля платы компьютера с тремя чипами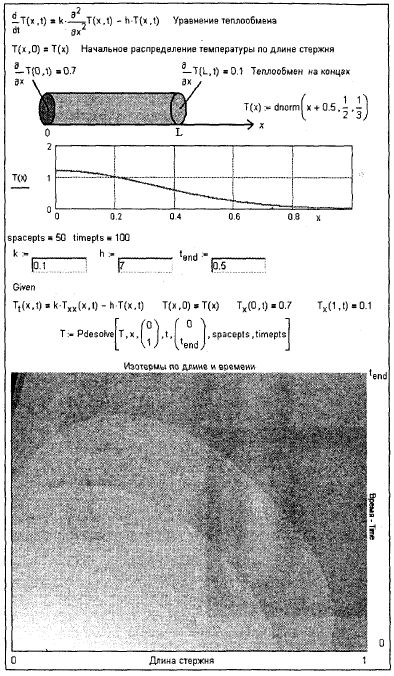

Рис. 5.25. Моделирование процесса остывания стержня

Суть задачи, показанной на рис. 5.25. В начальный момент времени (т=о) температура в стержне имеет значение т (х), где х — длина стержня, меняющаяся от 0 до 1. Стержень одним концом прижат, например, к микросхеме компьютера (см. выше) для его дополнительного охлаждения. Тут задействована функция denorm, отвечающая за нормальное (norm) распределение {d__

distribution). Читатель, зайдя на сайт задачи об остывающем стержне по адресу http://twt.mpei.ac.ru/mas/worksheets/pde_Temperature.mcd, может задать по точкам иное температурное поле в начальный момент. Кроме того, можно менять значение коэффициентов к и h, определяющих интенсивность теплопередачи внутри стержня и от поверхности стержня в окружающую среду, а также конечное время наблюдения за остыванием стержня tend. В задаче, показанной на рис. 5.25, как и в случае с функциями Find или Min(Max) imize, условие зажато между ключевым словом Given и встроенной функцией-решателем Pdesolve: само дифференциальное уравнение, где частные производные отмечаются текстовыми индексами (т. t — первая производная по времени, Tт.хх— вторая производная по длине стержня), и начальные условия: начальное температурное поле, вернее, температурная "линия" и то, что теплообмена на краях стержня нет— они заизолированы. Визуализация (а это, повторяем, очень часто выступает как ключевой момент в решении дифференциальных уравнений) на рис. 5.25 ведется через линии уровня. На сайте задачи (см. его адрес выше) они окрашены в цвета, имитирующие некое накаливание и остывание стержня.

Возвращаясь к началу главы — к ее своеобразному предисловию, — следует отметить, что в среде Mathcad некоторые дифференциальные уравнения можно решить аналитически, опираясь на команды и операторы символьной математики Mathcad/Maple. Так на рис. 5.26 показано, как в исходном дифференциальном уравнении y'=ky(Sat-y) вручную ведется разделение переменных (первая строка на рис. 5.26), а затем двумя действиями символьной математики (взятие интеграла и решение аналитического уравнения) формируется функция пользователя — решение дифференциального уравнения.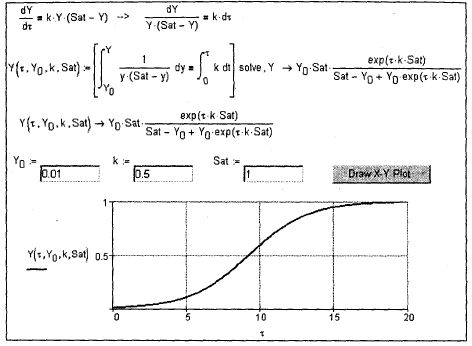

Рис. 5.26. Решение дифференциального уравнения средствами символьной математики

На рис. 5.26 показано и проиллюстрировано графиком решение так называемой логистической задачи, к которой сводятся многие физические, социальные и прочие явления: зарождение и медленное пробивание в жизнь (y0 — левая часть графика), более-менее бурное развитие (к — середина графика) и насыщение (sat — правая половина графика). Это зафиксировано дифференциальным уравнением y'=k*y (Sat-y): скорость роста зависит от самого роста двояко — в какой-то момент (у) процесс ускоряется, а в какой-то иной (sat-y) — замедляется. На рис. 5.26 все до предела упрощено, зато наглядно.