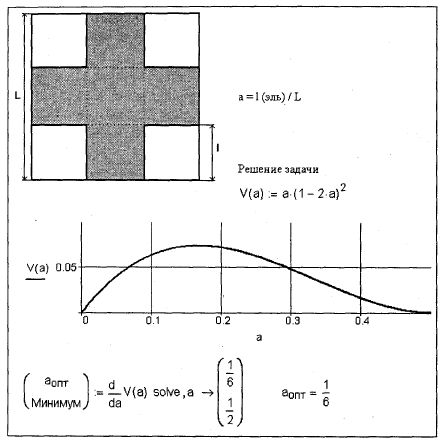
Задача о максимальном объеме коробки

Теперь решим задачу, подобную задаче о пожарном ведре, но более простую и более известную (см., например, Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления // Том 1.— М.: Физматлит, 2003. http://lib.mexmat.ru/books/34) задачу о максимальном объеме коробки (рис. 3.8). Она тоже будет иметь интересное продолжение, связанное с "утилизацией отходов раскроя".

У квадратной жестянки по углам вырезаются четыре квадрата. Полученная таким образом крестообразная заготовка сгибается в прямоугольную призму без верхней крышки, а четыре шва свариваются (паяются). Требуется рассчитать размер сторон вырезаемых квадратов (а лучше — отношение размеров квадратов а, чтобы отойти от конкретных размеров), при котором объем нашего "квадратного ведра" (коробки) будет максимальным.

На рис. 3.8 показано графическое и аналитическое решения задачи. Они отличаются от аналогичных решений по пожарному ведру (см. рис. 3.1 и 3.2) только видом анализируемой функции.

Продолжение задачи о коробке также похоже на продолжение задачи о пожарном ведре: обрезки идут на изготовление новых четырех коробок, новые обрезки (их уже будет 16) тоже пойдут в дело, и так до бесконечности. Но до нее (до бесконечности) мы доберемся чуть позже (см. рис. 3.10), сейчас же мы ограничимся только первыми тремя шагами раскроя квадратной заготовки (рис. 3.9).

Задача о коробках хороша тем, что в ней можно рассматривать любое число переменных оптимизации. Кроме того, сам процесс оптимизации можно в свою очередь также оптимизировать — оптимизация оптимизации, оптимизация в квадрате, если так можно сказать.

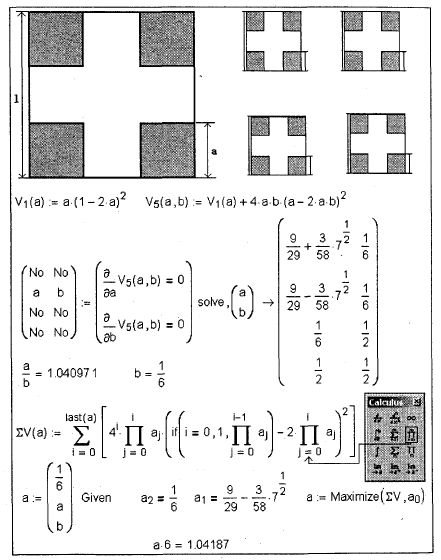
Рис. 3.8. Задача об оптимальном раскрое коробки

Формулу, по которой высчитывается суммарный объем коробок, можно сделать либо с переменным числом аргументов (функции V1 и v5 на рис. 3.9), либо с одним аргументом-вектором (функция sv). Второй вид записи (sv) более труден для вывода и анализа, зато более универсален — он позволяет делать расчет по любому количеству шагов раскроя. Для этого достаточно (только) менять длину вектора-аргумента функции sv. Слово "только" заключено в скобки потому, что в этом расчете свою роль может сыграть точность численной математики Mathcad. Здесь нужно будет менять не "только" число шагов раскроя, но и еще и методы расчета. Но это уже другая тема.

На рис. 3.9 оптимизация раскроя сделана двумя методами. Для функции v5 (два шага раскроя — пять коробок) решение найдено символьной математикой через поиск корней системы двух уравнений, включающих частные производные функции v5 по переменным а и ь. Для функции sv (три шага раскроя— 21 коробка) решение найдено через численную математику и через сведение задачи с тремя неизвестными к задаче с одной неизвестной с опорой на решения, найденные в задаче с двумя неизвестными. Это один из основных принципов математики.

Рис. 3.9. Задача об оптимальном раскрое пяти коробок

Рис. 3.10. Решение задачи о бесконечном числе коробок

Примечание

Символ частной производной преобразуется из символа "простой" производной через соответствующую команду контекстного меню, вызываемого щелчком правой кнопкой мыши на знаке производной.

На рис. ЗЛО даны решения задачи о бесконечном числе шагов раскроя коробок в двух вариантах: пропорция раскроя а не меняется (верхняя часть рис. 3.10) и пропорция раскроя меняется (но не а, b, с и т.д., а а0, a1, a2 и т. д. — элементы вектора а), а задача сводится к поиску оптимума функции с бесконечным числом аргументов.

При фиксированной пропорции раскроя (верхняя часть рис. 3.10) оптимум находится за счет упрощения выражения — через замену бесконечной суммы на несложное выражение.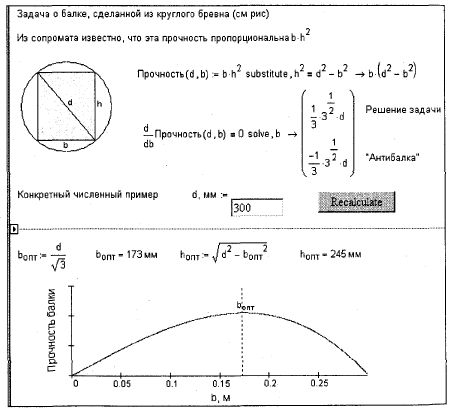

Рис. 3.11. Решение задачи об оптимальном сечении балки

Для изменяющейся пропорции раскроя (нижняя часть рис. 3.10) решение8 представлено в виде рекуррентного выражения, первое значение которого (пропорция раскроя последней коробки в бесконечной цепи) равна 1/6 (см. рис. 3.8).

На рис. 3.11 дано решение типичной оптимизационной задачи из области .проектирования— нахождение размеров сечения прямоугольной балки максимальной прочности. Дано аналитическое решение.